Hướng Dẫn Chi Tiết Cách Tìm Tọa Độ Trực Tâm H Của Tam Giác ABC
Trong hình học phẳng, trực tâm là một trong những yếu tố quan trọng của tam giác, có nhiều ứng dụng trong việc giải các bài toán hình học. Hôm nay, chúng ta sẽ tìm hiểu chi tiết về cách xác định tọa độ trực tâm H của một tam giác ABC.

1. Khái Niệm Cơ Bản Về Trực Tâm
1.1. Định nghĩa trực tâm
Trực tâm H của tam giác là giao điểm của ba đường cao trong tam giác. Đường cao là đường thẳng đi qua một đỉnh và vuông góc với cạnh đối diện (hoặc đường thẳng chứa cạnh đối diện).
1.2. Tính chất của trực tâm
- Trực tâm là điểm đặc biệt của tam giác
- Mọi tam giác đều có một và chỉ một trực tâm
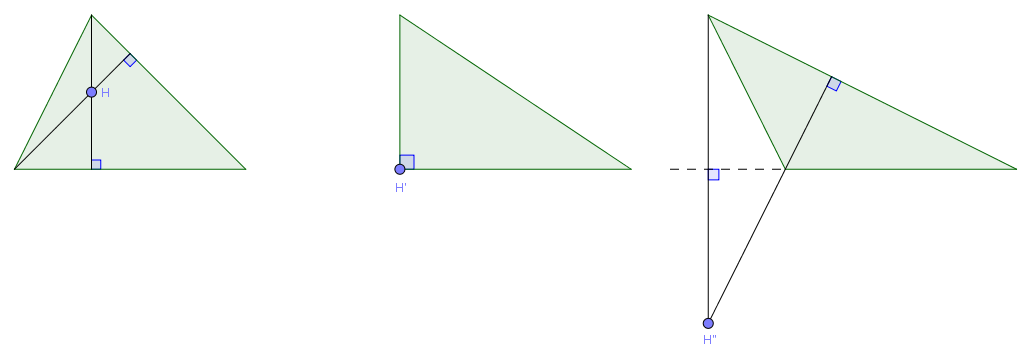
- Trong tam giác vuông, trực tâm trùng với đỉnh góc vuông
- Trong tam giác tù, trực tâm nằm ngoài tam giác
- Trong tam giác nhọn, trực tâm nằm trong tam giác

2. Phương Pháp Tìm Tọa Độ Trực Tâm
2.1. Công thức tổng quát
Để tìm tọa độ trực tâm H(xH, yH) của tam giác ABC với các đỉnh có tọa độ:
- A(x₁, y₁)
- B(x₂, y₂)
- C(x₃, y₃)
Ta sử dụng công thức:
xH = (a²(x₁ + x₂ + x₃) - b²x₁ - c²x₂ - a²x₃)/(a² + b² + c²)
yH = (a²(y₁ + y₂ + y₃) - b²y₁ - c²y₂ - a²y₃)/(a² + b² + c²)Trong đó:
- a, b, c là độ dài các cạnh của tam giác
- (x₁, y₁), (x₂, y₂), (x₃, y₃) là tọa độ các đỉnh A, B, C
2.2. Các bước thực hiện
- Xác định tọa độ ba đỉnh của tam giác
- Tính độ dài các cạnh của tam giác
- Thay số vào công thức tổng quát
- Tính toán và rút gọn kết quả
3. Ví Dụ Minh Họa
3.1. Bài toán mẫu
Cho tam giác ABC có tọa độ các đỉnh:
- A(1, 2)
- B(4, 1)
- C(2, 5)
Tìm tọa độ trực tâm H của tam giác.
3.2. Cách giải
Bước 1: Tính độ dài các cạnh
a = BC = √[(4-2)² + (1-5)²] = √20
b = AC = √[(2-1)² + (5-2)²] = √10
c = AB = √[(4-1)² + (1-2)²] = √10Bước 2: Thay số vào công thức
xH = (20(1 + 4 + 2) - 10(1) - 10(4) - 20(2))/(20 + 10 + 10)
yH = (20(2 + 1 + 5) - 10(2) - 10(1) - 20(5))/(20 + 10 + 10)Bước 3: Tính toán
xH = 2.5
yH = 2.75Vậy tọa độ trực tâm H là (2.5, 2.75)

4. Một Số Lưu Ý Quan Trọng
4.1. Điều kiện tồn tại
- Tam giác phải thực sự tồn tại (tổng hai cạnh bất kỳ phải lớn hơn cạnh còn lại)
- Ba điểm A, B, C không được thẳng hàng
4.2. Kiểm tra kết quả
- Vẽ hình để kiểm chứng
- Sử dụng phần mềm hình học động để xác minh
- Kiểm tra tính hợp lý của kết quả
5. Ứng Dụng Thực Tế
5.1. Trong giáo dục
- Giải các bài toán hình học phẳng
- Xây dựng các bài toán nâng cao
- Phát triển tư duy không gian
5.2. Trong thực tiễn
- Thiết kế và xây dựng
- Định vị và đo đạc
- Ứng dụng trong công nghệ và kỹ thuật
Kết Luận
Việc tìm tọa độ trực tâm H của tam giác ABC là một kỹ năng quan trọng trong hình học phẳng. Thông qua việc nắm vững phương pháp và thực hành nhiều bài tập, học sinh sẽ phát triển được tư duy logic và khả năng giải quyết vấn đề trong toán học.
Để cập nhật thêm nhiều kiến thức bổ ích về toán học và các môn học khác, vui lòng truy cập:
Website: websitegiaoduc.com
Hotline: 0901 02 03 04
Email: [email protected]
Bài viết được tổng hợp và biên soạn bởi đội ngũ chuyên gia của Website Giáo Dục – Nơi chia sẻ kiến thức, kinh nghiệm và tài liệu giáo dục chất lượng.












0 Comment